算法分析

程序与算法的区别：

算法：对解决问题的分步描述。
程序：采用某种编程语言实现的算法，同一个算法可以有多种程序来实现。

评价程序的”好坏“有众多因素，如：

代码风格

Python的强制缩进，实现了语句块功能和视觉效果的统一。
可读性
可维护性

这里主要感兴趣的则是算法本身的特性，从计算资源消耗的角度来评判和比较算法：

好算法能更高效利用计算资源，或更少占用计算资源来解决问题。

计算资源指标主要有：

解决问题所需的存储空间或内存；

但存储空间受到问题自身数据规模的变化影响，需要区分哪些存储空间是问题本身描述所需的，哪些是算法占用的。
解决问题所需的执行时间。

更常使用的评价指标。

Python中有一个time模块（t1 = time.time()），可以获取计算机的当前时间，因此可以在算法开始前和结束后分别记录系统时间，做差即可得到运行时间。t1是一个浮点数，单位是秒，记录了从1970年1月1日00:00:00到现在所走过的时间。或者使用timeit中的Timer。

但关于运行时间的实际检测是存在问题的，即检测结果受到编程语言和运行环境的影响。

因此，需要有更好的指标来衡量算法的好坏，而这个指标与具体的机器、程序、运行时段都无关。

大O表示法

算法时间度量指标：评估一个算法所实施的操作数量或步骤数。这需要一种通用的基本操作来作为运行步骤的计量单位，使其可以摆脱程序或计算机的影响来描述算法的效率。

赋值语句是一个合适的选择。换言之，将每一次赋值操作看成基本计算单位，那么算法的执行时间便可通过解决问题所需的步骤数来衡量。

一条赋值语句同时包含了（表达式）计算和（变量）存储操作。

除了与计算资源无关的定义语句外，主要就是控制流语句和赋值语句。而控制流语句仅仅起到了组织语句的作用，并不实施处理。

以如下的求前 $n$ 项和函数为例：

def sum_of_n(n):
    the_sum = 0 # 赋值语句，执行1次
    for i in range(1, n+1): # 控制流语句，执行n次
        the_sum = the_sum + i # 复制语句，执行1次
    return the_sum

该函数的问题规模为： $n$ ；
赋值语句数量为： $T(n) = 1+n\times 1 = 1 + n$ ；

问题规模是影响算法执行时间的主要因素。因此，在累计求和sum_of_n的算法中，需要累计的整数个数 $n$ 就是问题规模。

算法分析的目标：找出问题规模会怎么影响一个算法的执行时间。

数量级函数

基本操作数量函数 $T(n)$ 的精确值并不是特别重要，重要的是 $T(n)$ 中起决定性因素的主导部分。

即，当问题规模增大时，只有某些项会极大影响执行时间，其他项可以忽略不计。

那么，这里引入了数量级（order of magnitude）描述，其描述了 $T(n)$ 中随着 $n$ 增加而增加速度最快的主导部分。

这种数量级表示法即称作大O表示法，记作 $O\left(f(n)\right)$ ，其中 $f(n)$ 表示 $T(n)$ 中的主导部分， $O$ 表示order。

这种数量级也可以称为渐进时间复杂度（asymptotic time complexity），简称时间复杂度。

$f(n)$ 为 $T(n)$ 函数中起决定性作用的部分提供了简单的表示。

大致理解为找到一个 $f(n)$ ，使得 $\lim_{n\rightarrow\infty}\dfrac{T(n)}{f(n)}=\text{Const.} \neq 0$ 。那么，该算法的时间复杂度称为 $O(f(n))$ 。

算法1的基本操作数量： $T(n) = 1 + n$ 。

当n增大时，常数部分可以忽略不计，因此， $f(n) = n$ ，那么该算法的运行时间数量级为 $O(n)$ 。

$\lim_{n\rightarrow\infty}\dfrac{T(n)}{f(n)}=\lim_{n\rightarrow\infty}\dfrac{1+n}{n}=1$

算法2的基本操作数量： $T(n) = 5n^2 + 27n + 1005$ 。

当 $n$ 很小时， $1005$ 起决定性作用；
当 $n$ 越来越大时， $n^2$ 项越来越重要，其他两项对结果的影响越来越小；
忽略系数。

因此， $f(n)=n^2$ ，那么运行时间数量级为 $O(n^2)$ 。

$\lim_{n\rightarrow\infty}\dfrac{T(n)}{f(n)}=\lim_{n\rightarrow\infty}\dfrac{5n^2 + 27n + 1005}{n^2}=5$

另外，有时决定运行时间的并不仅仅是问题规模，还有其他因素，如某些特定的具体数据也会影响算法运行时间。

因此，算法的性能其实可以分为最好、最差和平均情况，而平均情况体现了算法的主流性能。

不要被某些特定的运行情况所迷惑。例如，输入给排序算法的数据为已排序好的数据。

常见的大O数量级函数

通常当 $n$ 较小时，难易确定其数量级；
当 $n$ 增长较大时，容易看出主要变化。

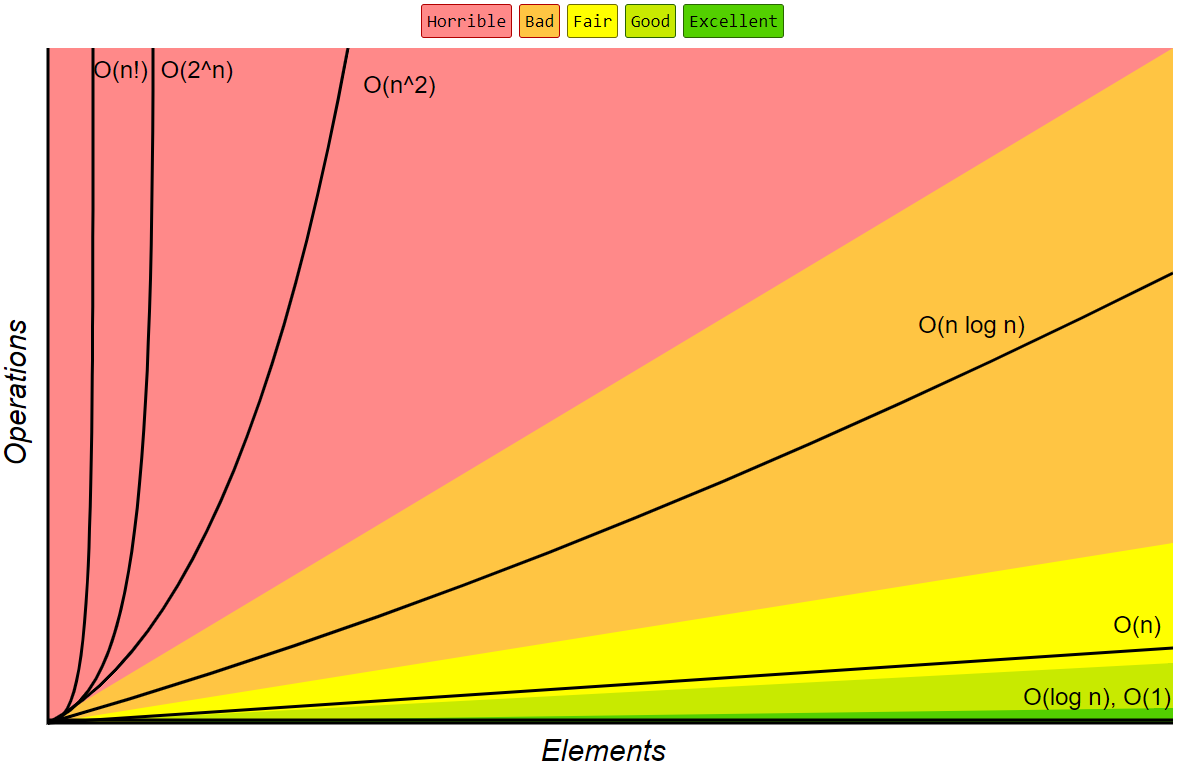
一般常见的大O数量级函数如下：

$f(n)$	名称	直观理解
$1$	常数阶
$\log(n)$	对数阶	每操作1次，需要处理的规模就小一半；随着问题规模翻倍，操作次数只增加1次。例如二分查找法。
$n$	线性阶	常见于循环。
$n\log(n)$	对数线性阶	循环 $n$ 次时间复杂度为 $O(\log n)$ 的算法。例如排序算法。
$n^2$	平方阶	常见于循环。
$n^3$	立方阶
$2^n$	指数阶

示意图如下：
常见的大O数量级函数

案例分析

分析如下代码的执行时间数量级函数（时间复杂度）：

a = 5
b = 6
c = 10
for i in range(n):
    for j in range(n):
        x = i * i
        y = j * j
        z = i * j
for k in range(n):
    w = a * k + 45
    v = b * b
d = 33

可以得到赋值操作的数量为： $T(n) = 3 + 3n^2 + 2n + 1 = 3n^2 + 2n + 4$ 。

因此，该算法的时间复杂度为 $O(n^2)$ 。

由内向外分析。其实找到时间复杂度最大的循环结构便可。

变位词判断问题

变位词：两个词之间存在组成字母的重新排列关系。

如heart与earth，god与dog。

为了简单起见，假设参与判断的两个词仅由小写字母构成，而且长度相等。

解题目标：编写一个bool函数，输入两词，返回这两个词是否为变位词。

思路：

以词1为模板，检查词2中是否存在对应的字符；
利用标记，防止重复检查；
若每个字符都能对应找到，则两词为变位词；
只要有一个字符找不到，则不是变位词。

def is_anagram(s1, s2):
    search_char = list(s2) # 复制到列表中，这样才能进行“标记”（即修改值为None）
    pos_template = 0
    is_anagram = True
    while pos_template < len(s1) and is_anagram: # 循环s1中每个字符
        pos_search = 0
        is_identical = False
        while pos_search < len(search_char) and not is_identical: # 对s2的各个字符进行对比
            if search_char[pos_search] == s1[pos_template]:
                is_identical = True
            else:
                pos_search = pos_search + 1
        if is_identical:
            search_char[pos_search] = None # 如找到字符，则进行标记
        else:
            is_anagram = False # 只要有一个字符没找到，则不是变位词
        pos_template = pos_template + 1
    return is_anagram

分析：

问题规模：词中包含的字符个数 $n$ ；
时间复杂度： $O(n^2)$ 。

主要在于两重循环：

外层循环遍历s1的每个字符，循环了 $n$ 次；

内层循环在s2中查找字符，每次查找的次数 $\in\{1,2,\cdots,n\}$ 。（找到对应字符便结束循环，并不是遍历s2）。

因此，总执行次数 $T(n)=\dfrac{n(n+1)}{2}=\dfrac{1}{2}n^2 + \dfrac{1}{2}n$ ，则 $f(n)=n^2$ ，因此数量级为 $O(n^2)$ 。

思路：

将两个字符串都按照字母顺序排好；
再逐个字符比较是否相同。

def is_anagram(s1, s2):
    s1_list = list(s1)
    s2_list = list(s2)
    s1_list.sort() # 列表的内置函数，直接改变了列表值的顺序
    s2_list.sort()
    pos = 0
    is_identical = True
    while pos < len(s1) and is_identical:
        if s1_list[pos] == s2_list[pos]: # 对排序后的列表进行逐个对比
            pos = pos + 1
        else:
            is_identical = False
    return is_identical

分析：

粗看，从解法1的两重循环变成了单个循环，数量级是 $O(n)$ ；
但是，sort()的代价并不等同于基本赋值操作的代价，后续会分析大部分排序算法的数量级是 $O(n^2)$ 或 $O(n\log(n))$ ，大过循环的 $O(n)$ ；
因此实际上，解法2的时间复杂度等于排序算法的复杂度，即 $O(n\log(n))$ 。

这里以时间复杂度为 $O(n\log(n))$ 的排序算法为例， $O(n\log(n) + n) = O(n\log(n))$ 。

思路：穷尽所有可能的组合，将s1中出现的字符进行全排列，再查看s2中是否出现在全排列列表里。

困难：产生s1所有字符的全排列，其所有可能的字符串有 $n!$ 个。

然而，对于20个字符长的词来说，将产生 $20!=2,432,902,008,176,640,000$ 个候选词，如果每微秒处理1个候选词，则需要近8万年时间才能做完所有匹配。

因此，暴力法并不是合适的算法。

思路：

对比两词中每个字母出现的次数，如果26个字母出现的次数都相同，则是变位词；
为每个词设置一个26位的计数器，检查每个词，在计数器中记录每个字母出现的次数；
比较两个词对应的计数器是否相同，若相同，则是变位词。

def is_anagram(s1, s2):
    counter1 = [0] * 26 # 初始化两个长度为26的计数器
    counter2 = [0] * 26
    for i in range(len(s1)):
        pos = ord(s1[i]) - ord('a') # 将字符转变为ASCII数值，记录该字符的对应位置
        counter1[pos] = counter1[pos] + 1 # 计数器对应位置加1
    for i in range(len(s2)):
        pos = ord(s2[i]) - ord('a')
        counter2[pos] = counter2[pos] + 1
    is_identical = True
    pos = 0
    while pos < 26 and is_identical: # 计数器比较
        if counter1[pos] == counter2[pos]:
            pos = pos + 1
        else:
            is_identical = False
    return is_identical

分析：

虽然有3个循环，但并不是循环嵌套；
因此，总执行次数为 $T(n)=2n+26$ ，则时间复杂度为 $O(n)$ ；

该算法为这四种解法中性能最优；

但是，这付出了存储空间的代价，若考虑的是大字符集构成的词，还会需要更多的存储空间，而不仅仅是长度只有26的计数器列表。
牺牲存储空间换来运行时间，或牺牲运行时间换来存储空间，这种在时间和空间之间的取舍和权衡，在选择问题解法的过程中会经常出现。

中文也有类似的“变位词”：“不可随处小便”，“小处不可随便”。
当然可以使用“字典”这种结构作为计数器，那样就不需要使用ord这个函数。

空间复杂度

评估解决问题所需的存储空间或内存的大小。

分析目标：找出问题规模如何影响一个算法所需的内存大小。

分析思路：

看声明的变量；
看是否有递归。（因为变量会一直保存在递归栈中）

如

def sum_n(num):
    total = 0
    for i in range(1,num+1):
        total += i
    return total

问题规模为num；
主要变量为total，其为int类型（其占用内存空间的大小与num无关）。

因此上述算法的空间复杂度为 $O(1)$ 。

常用到的时间复杂度： $O(1)$ 、 $O(n)$ 、 $O(n^2)$ 。

Python数据类型的性能

讨论Python两种内置数据类型上各种操作的大O数量级：列表（list）和字典（dict）。

类型	list	dict
索引	自然数i	不可变类型值key
添加	`append`、`extend`、`insert`	`b[key] = v`（无次序关系，直接利用key进行赋值）
删除	`pop`、`remove`*	`pop`
更新	`a[i] = v`	`b[key] = v`
正查（根据索引来得到数据项）	`a[i]`、`a[i:j]`	`b[k]`、`copy`
反查（根据数据项来得到索引）	`a.index(v)`、`a.count(v)`	无
其他	`reverse`（倒排）、`sort`	`has_key`、`update`

List列表数据类型

list类型各种操作（interface）的实现方法有很多，选择准则为：让最常用的操作性能最好，牺牲不太常用的操作。

80/20准则：80%的功能其使用率只有20%。

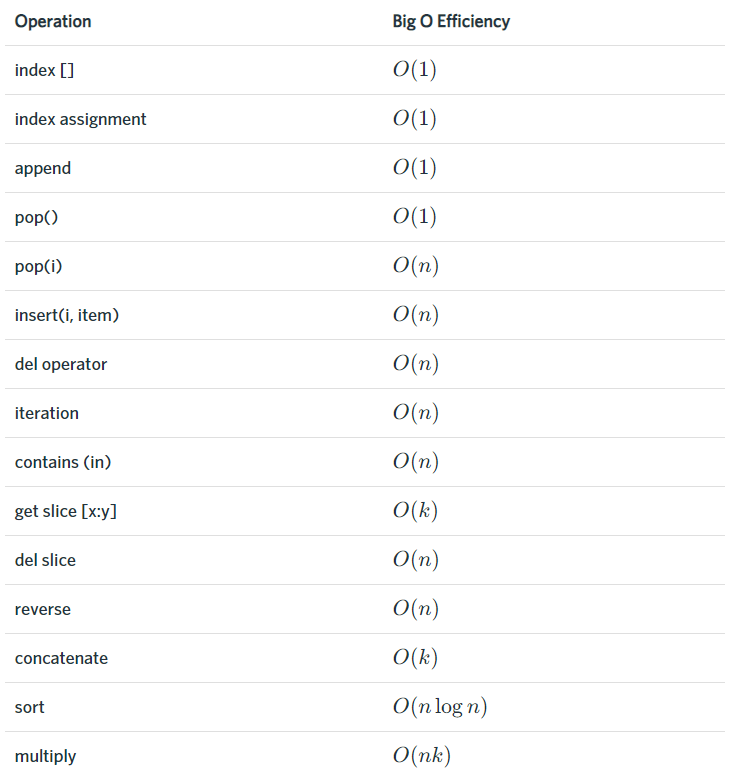
常用操作性能：

按索引取值（v = a[i]）和赋值（a[i] = v）：由于列表的随机访问特性，这两个操作执行时间与列表大小无关，均为 $O(1)$ ；
列表增长：
- lst.append(v)： $O(1)$ ；
  
  （直觉）只需要读取到列表最后一个元素的位置，并在其追加新元素即可。
- lst = lst + [v]： $O(n+k)$ ，其中 $k$ 是被加的列表的长度。
选择哪个方法来操作列表，决定了程序的性能。

List基本操作的大O数量级

图源：Practical Algorithms and Data Structures

Dict字典数据类型

字典与列表的主要不同：

字典是根据关键码（key）找到数据项；
列表是根据位置（index）找到数据项。

字典最常用的操作：

取值get和赋值set： $O(1)$ ；
判断字典中是否存在某个关键码contains (in)： $O(1)$ 。

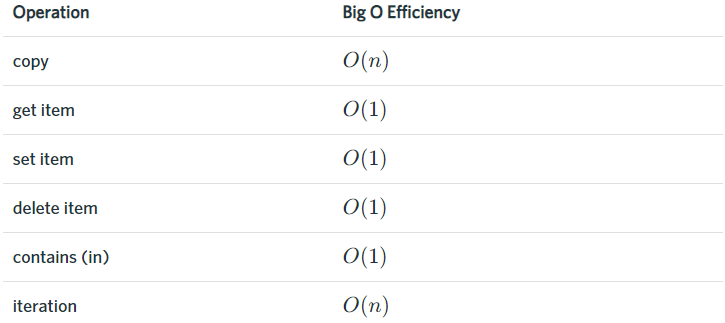
Dict基本操作的大O数量级

图源：Practical Algorithms and Data Structures

更多Python数据类型操作复杂度可以参考：https://wiki.python.org/moin/TimeComplexity。

OJ做题注意事项

OJ：Online Judge，在线判题。

一个程序具有如下3个要素（IPO）：

Input
Process
Output

检查算法程序的正确性：

给定几个测试用例的输入数据
程序处理这些数据
程序输出结果，并与答案对比

人工评测过程：

手工输入：data = input()
肉眼检查：print(result)

自动在线评测即让OJ评测机接管程序代码中的input和print，然后收集所有输出与测试用例的答案对比，只有完全一致才能通过。

做题注意：

从题意得出IPO信息；
看清样例格式；
编写程序。

其中，要注意输入输出格式，

对于输入：
- 多行输入，每行对应一个input()函数，根据题目描述的输入类型转换；如需要整数，则可使用a = int(input())。
- 单行多个变量，可用input().split()读入并分解为列表；如需要整数，则可使用list(map(int, input().split()))。
input().split()：这样输入得到的列表每个元素为字符；

map(function, list1, ...)：根据提供的函数对指定序列做映射，返回迭代器。
对于输出：
- 单个整数，直接print即可；
- 若是浮点数，则要看清保留小数点几位，进行格式化输出。
- 注意空格的位置和数量，行末一般不输出空格。