基本概念

数据类型：
- 数据类型是一种在程序员和编译器两者之间传输的信息类型，使编译器了解所要存储的数据的类型，以及所需占据的内存空间的大小。
- 用来分类数据，描述具有相同属性的数据。
- 表示变量的类型，其定义了特定变量将被分配所给定的数据类型的值。
  
  基本例子就是程序中所使用的各种变量的类型，如int、char、string。
  
  也可自己定义数据类型，例如自己实现的数据结构就可以作为一种数据类型。
数据结构：
- 存在一种或多种特定关系的数据元素的集合。
  
  具有不同形式和不同类型的数据元素的集合，这些数据可以被某些操作所处理。
- 数据结构是数据项的结构化集合，其结构性表现为数据项之间的相互联系及作用，也可以理解为定义于数据项之间的某种逻辑次序。
- 数据结构具有可执行的特定的操作（如插入、删除和遍历），整个数据可以用一个对象（object）来表示，并且可以在整个程序中使用。
  
  例如，当需要存储大量个人数据（包括姓名、年龄、电话等信息）时，这种类型的数据需要复杂的数据管理，这意味着其需要多个基本（原始）数据类型所组成的数据结构来帮助数据管理，保证对数据的运算或操作能够高效实现。此时，可称这种数据结构是一种数据类型。
- 根据逻辑次序的复杂程度，可以将各种数据结构划分为线性结构、半线性结构与非线性结构三大类。
抽象数据类型：
- 一个数学模型以及定义在此数学模型上的一组操作，仅具有功能的描述和实现功能的接口。
- 数据结构是抽象数据类型（所提供的规范）的具体实现（concrete implementation）。
  
  例如，对栈、队列、图等概念的学习就是对某一种抽象数据类型的学习。
- 抽象数据类型的实现可以采用不同的方式。
  
  例如，可以使用数组或链表等数据结构来完成对ADT队列的实现。

Python内置的数据类型

基本数据类型

Number 数字

主要有四种类型：int（整型）、float（浮点数）、complex（复数）、bool（布尔值）。

运算：+、-、*、/、//（整除）、%（取余）。

常用函数：abs(n)（取绝对值）、max()、min()、power(x,y)（ $x^y$ ）、sqrt()（不属于Python的内置函数，需要import math）。

内置数据类型

List 列表

Python中的List列表其实是向量（DSA-03-linear-structure）。

后续对于List的指代若无特别说明，均指Python中的List数据结构。

用法：用[]括起来的数据集。

索引是从0开始的。

里面的元素可以是相同类型或不同类型的元素。

List中涉及到的几个主要操作：

a[index]：正查（访问），index指索引；
a.index(value)：反查（搜索），找到value的索引；
a.append(item)：增加元素，item指要在末尾加入的新元素；
a[index] = new_data：更新元素；
a.pop()：删除末尾元素，返回值为被删除的元素；
a.pop(index)：删除指定index位置的元素，返回值为被删除的元素；
value in a：判断列表a中是否有value，返回bool值；
a.reverse()：a的元素颠倒排序，a[::-1]也可实现；
a.clear()：清除a中所有元素。
切片slice操作：a[0:3]展示索引从0到2的元素。

x:y：左闭右开区间，即 $[x,y)$ ；

a[1:-1]：-1表示最后一个元素的索引，但是这个slice取不到最后一个元素；

a[1:]：:之后没写，默认是从指定索引取到最后一个元素；

a[:]：:前后都没有值，默认是取所有元素。

常用函数：

len(a)：报告列表的规模；
max(a)：取列表中最大值；
min(a)：取列表中最小值；

遍历/迭代List：

# 直接遍历列表的元素
for i in a:
    print(i)
<!--code0-->

> `range(x,y)`：是左闭右开区间，即$[x, y)$

List comprehension（列表推导式）：

列表推导式，对可遍历对象中的每个元素进行同一个操作或运算。

[expression for element in iterable_object]，如：

b = [i * i for i in a]
>>> b = [1, 4, 9, 16, 25]

[expression if condition else statement for element in iterable_object]，如：

b = [i * i if i < 3 else i for i in a] # 只有满足条件的元素才运算
>>> b = [1, 4, 3, 4, 5]

Tuple 元组

用法：用()括起来的数据集。

里面的元素可以是相同类型或不同类型的元素。

List与Tuple的区别：

List支持：增、删、改、查；
Tuple支持：查（即，无法修改集合中的内容）。

Tuple主要用在查的情况！避免误操作修改了集合中的内容。

Tuple的查找：

a[index]：正查，返回索引为index的元素值；
a.index(value)：反查，返回value的索引。

常用操作（与List一样）：

value in a：判断列表a中是否有value，返回bool值；
切片slice操作；
遍历/迭代操作。

常用函数：

len(a)：报告元组的规模；
max(a)：取元组中最大值；
min(a)：取元组中最小值。

注意：

当a = (1)时，a是int类型；
当a = (1,)时，a是tuple类型；

Set 集合

用法：用{}括起来的数据集，且其中所有的元素是唯一的。

Set中的元素是无序的，即不是按照索引来获取（访问）对应值的。

理解成：圈养了独一无二的一堆数。这种结构比较非主流。

Set中涉及到的几个主要操作：

a = set()：创建集合；
a.add(item)：增加元素，添加一个元素item；

如果Set中已经有item，那么改Set不会变。
a.update(iteratable_object)：增加多个元素（可迭代数据类型中的元素值）；
a.remove(value)：删除元素value；

在Set中，用a.pop()没啥意义，因为Set无索引。
item in a：判断是否存在某个元素，返回bool值。

Set中涉及到的几个常用运算：

-：如a - b指a有b没有的元素（差集）；
|：如a | b指a有或b有的元素（并集）；
&：如a & b指a有且b有的元素（交集）；
^：如a ^ b指a和b中不同时有的元素（并集减交集）

常见的set：HashSet（比较常见）、LinkListSet、TreeSet。

Dictionary 字典

用法：用{}括起来，元素为键-值对（key:value）。

如a = {"name":"learning", "age":18}。

Dictionary中涉及到的几个主要操作：

a[key]：正查，利用key来查；

相当于给set加了个索引信息，这个索引信息就是key。
a[key] = value：增加（修改）key索引的值为value；
a.pop(key)：删除索引为key，值为value的键值对；
key in a：判断是否存在某个键key，返回bool值。

注：字典的in操作是判断是否存在指定的”字“（键key），而不是判断是否存在指定的值（value）；

遍历/迭代Dictionary：

for key in a: # 只有a表示只看key
    print(key) # 遍历键key
    
for value in a.values(): # a.values()表示看a中的所有值
    print(value) # 遍历值value
    
for k,v in a.items(): # a.items()表示看a中的所有元素（键-值对）
    print(k,v) # 遍历键-值对

String 字符串

用法：用""引起来的内容，其中每个元素为字符。即，由一个个字符所组成的数组。

String中涉及到的几个主要操作：

正查、切片操作；
a.count(s)：计数字符s出现了多少次；
a.isupper()：判断a中的字母是否全为大写字母，返回bool值；
a.islower()：判断a中的字母是否全为小写字母，返回bool值；
a.isdigit()：判断a中的字符是否全为数字字符，返回bool值；
a.upper()：返回将a中的字母改为大写的结果，a没有被修改；
a.lower()：返回将a中的字母改为小写的结果，a没有被修改；
a.strip()：返回将a中最前最后的空格删除的结果，a没有被修改；
a.lstrip()：返回将a中最前的空格删除的结果，a没有被修改；
a.rstrip()：返回将a中最后的空格删除的结果，a没有被修改；
a.swapcase()：返回将a中的字母大小写互换的结果，a没有被修改；
a.replace(old, new)：返回将a中的old字符（串）替换为new字符（串），a没有被修改；
a.split(seq)：返回根据分隔规则seq将字符串a进行分割的结果，a没有被修改。

a.split()：默认是以空格为规则来分隔，即a.split(" ")；

可以看到，String数据类型所提高的操作并没有像List那样修改原数组内容。通过这点可以帮助记忆，String类型的元素是不支持修改的。

常用函数：

len(a)：报告字符串的规模；
max(a)：取ascii码最大的字符；
min(a)：取ascii码最小的字符。

常见数据结构

用Python实现常见数据结构时，除了使用某些包提供的数据类型，也可以自定义。

但这里均以已实现对应ADT接口的数据结构（已有轮子）为例进行介绍。

Array 数组

其元素类型相同，且需要用一块连续的内存空间来存储的数据集。

优点：正查（访问，access）的时间复杂度为 $O(1)$ ；

缺点：反查（search）、插入和删除的时间复杂度为 $O(n)$ 。

适合读，不适合写。

数组的扩展 $\rightarrow$ 向量。

用Python实现数组

可以用Python内置的List实现Array，只要List中的元素类型相同。

LinkedList 链表

# Definition for singly-linked list.
class ListNode:
    def __init__(self, x):
        self.val = x
        self.next = None

链表的元素是节点，每个节点包含两个信息（值和指向下一个Node的信息）。

优点：插入（仅针对插入这个操作）和删除的时间复杂度为 $O(1)$ ；

缺点：正查和反查的时间复杂度为 $O(n)$ 。

适合写，不适合读。

类型：有单端、双端链表。

链表的扩展 $\rightarrow$ 列表（非Python内置的那个List，见DSA-03-linear-structure的介绍）。

用Python实现链表

Python的deque就是一种链表。

需要from collections import deque

以其为例，常用操作如下：

linkedlist = deque()：创建链表；
linkedlist.append(item)、linkedlist.insert(pos, item)：添加元素item；

注意这里的insert()时间复杂度是 $O(n)$ ，因为这是实现插入的函数，还包括了查找到这个pos的时间。
linkedlist[index]：访问位置为index的元素；

时间复杂度为 $O(n)$ 。
linkedlist[index] = new_data：修改位置为index的元素；

时间复杂度为 $O(n)$ 。
linkedlist.index(item)：搜索元素item的位置；

时间复杂度为 $O(n)$ 。
linkedlist.remove(item)：删除元素item；

删除指定索引index上的元素则为：del linkedlist[index]；

时间复杂度也是 $O(n)$ ，还包括了查找到这个元素的时间。
len(linkedlist)：获取链表规模大小。

时间复杂度为 $O(1)$ 。

Hash Table 哈希表

通过哈希算法将key映射成唯一索引，来帮助访问对应的value。

优点：访问、添加、删除的时间复杂度为 $O(1)$ ；

读写性能都不错。

缺点：哈希碰撞；哈希表中的元素是无序的。

哈希碰撞：2个不同的key通过一个哈希函数得到相同的内存地址。解决方法：例如可以使用链表来解决。

用Python实现哈希表

Python的dictionary就是一种哈希表（散列表）。

Queue 队列

队列Queue：队列仅有一个入口和一个出口。

双端队列Deque：数据项既可以从队首加入，也可以从队尾加入；数据项也可以从两端移除。

先入先出（First-In First-Out, FIFO）；“行为绅士”；

主要用在BFS中。

用Python实现队列

Python的话可以使用deque。具体操作如下（也可以作为单端队列使用）：

需要from collections import deque

linkedlist = deque()：创建链表；
linkedlist.append(item)：添加元素item；

注意这里的insert()时间复杂度是 $O(n)$ ，因为这是实现插入的函数，还包括了查找到这个pos的时间。
linkedlist[index]：访问位置为index的元素；

时间复杂度为 $O(n)$ 。
queue[0]：获取即将出队的元素；

时间复杂度为 $O(1)$ 。

这里因为是双端队列，如果用作单独队列，就分清楚哪端是头，哪端是尾。
queue.popleft()：删除即将出队的元素；

时间复杂度为 $O(1)$ 。
len(queue)：获取队列规模；

时间复杂度为 $O(1)$ 。

遍历队列（一般是元素边出队边遍历）：

while len(queue) != 0:
    temp = queue.popleft()
    print(temp)

Stack 栈

数据项的加入和移除都仅发生在同一端（栈顶）。

后入先出（Last-In First Out，LIFO）；如浏览器后退功能。

主要用在DFS中。

用Python实现栈

可以直接用Python的List来实现栈的一些操作（选取栈顶为List的末尾，使用pop与append）。

Heap 堆

一种完全二叉树的结构，且每个节点 $\geq$ 子节点（最大堆/大根堆），或每个节点 $\leq$ 子节点（最小堆/小根堆）。

用Python实现小根堆

可以使用heapq包中的heapify来实现小根堆。

# 小堆
from heapq import heapify, heappush, heappop, nlargest, nsmallest

a = [1,2,3,4,5]
heapify(a) # 默认是小堆
heappush(a, 4) # 给堆a增加元素4
heappop(a) # 删除堆顶值
nlargest(2, a) # 返回a中前2个最大值
nsmallest(2, a) # 返回a中前2个最小值

heapq的包不支持大堆，如果要用大堆，那就把数组都乘 $-1$ ，然后用小堆来实现。

访问：无，一般不通过索引来访问堆中元素；

搜索：指只查看堆顶元素 $O(1)$ ；

添加： $O(\log n)$ ；

删除： $O(\log n)$ ；

构建过程分析：一堆无序的数 $\rightarrow$ 完全二叉树 $\rightarrow$ 最大堆/最小堆

第一个箭头过程： $O(n)$ ，只要遍历一次数组即可构建；
第二个箭头过程： $O(n)$ ，最差的情况就是每层元素需要一直往下去交换，相当于每层需要操作数=每层元素*单元素逐渐往下交换的次数（从该层走下最底层）。

Tree 树

连接的节点与节点之间有父子关系。

节点：

根节点：最祖先的那个节点；
叶子节点：无下一个子节点。

二叉树节点的空指针数 = 总节点数 + 1。

因为1个节点需要包含指向左右2个节点的指针，那么， $n$ 个节点的二叉树共需要 $2n$ 个指针域；

又因为连接 $n$ 个节点只需要 $n-1$ 条边（理解成：将树变成链状，其边数不会发生改变， $n-1$ 个子节点就需要 $n-1$ 个边），那么，需要占用 $n-1$ 个指针域；

所以，剩下的空指针域有 $2n-(n-1)=n+1$ 个。

由此，可以计算出对应的叶子节点个数为 $\left\lfloor \dfrac{n+1}{2} \right\rfloor$ （因为只有2个指针域都空才能算叶子节点，因此需要向下取整）。

那么，非叶子节点个数则为 $n - \left\lfloor \dfrac{n+1}{2} \right\rfloor$ 。

其他概念：

高度：节点到叶子节点的最长路径（最大边数）；

树的高度：根节点到叶子节点的最长路径。
深度：根节点到节点的边数；
层：同辈节点为一层，最祖先的节点为第一层。

二叉树：

普通二叉树：每个节点最多有两个子节点；
满二叉树：除了叶子节点，每个节点都有两个子节点（左右节点）；且每个叶子都在同一层；
完全二叉树：对树中的节点从上至下、从左至右编号，这些节点的编号与满二叉树节点的位置相同。（从上至下、从左至右依次填满）

想象满二叉树的右侧方缺少右节点的样子。

二叉树的遍历：

前序遍历：根节点 $\rightarrow$ 左子树 $\rightarrow$ 右子树
中序遍历：左子树 $\rightarrow$ 根节点 $\rightarrow$ 右子树
后续遍历：左子树 $\rightarrow$ 右子树 $\rightarrow$ 根节点

这个”序“看”根节点“来确定。

遍历示意如下：

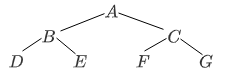
前序遍历： $A\rightarrow B\rightarrow D\rightarrow E\rightarrow C\rightarrow F\rightarrow G$

中-左-右
中序遍历： $D\rightarrow B\rightarrow E\rightarrow A\rightarrow F\rightarrow C\rightarrow G$

左-中-右
后续遍历： $D\rightarrow E\rightarrow B\rightarrow F\rightarrow G\rightarrow C\rightarrow A$

左-右-中

用Python实现树

创建树的话，可使用一个队列来记录父节点，遍历指定数组并将其元素压入父节点队列，每当一个子树构建完成后，将队列中的首父节点弹出。

需要注意：是树节点（class TreeNode）为None，还是树节点的value为None。

Graph 图

节点与节点之间不是父子关系，其可理解为朋友或邻居关系。

从某个节点到某个节点可能不止一条路径。

重要概念：

顶点、邻居节（顶）点；
边：连接节点与节点的线；
度（degree）：每条边可以指一度（如，邻居是一度关系，邻居的邻居是二度关系）；
无向图
有向图：节点与节点之间有指向关系（如，A关注B，B没有关注A）；
- 入度：多少边指向该顶点；
- 出度：多少边从这个点为起点指向别的顶点。
权重图：边是有权重的（如，A与B之间的路径，路径长度就是边的权重）

求最短路径的常见算法：Bellman-Ford算法、Dijkstra（狄克斯特拉）算法

DFS（深度优先搜索）、BFS（广度优先搜索）。